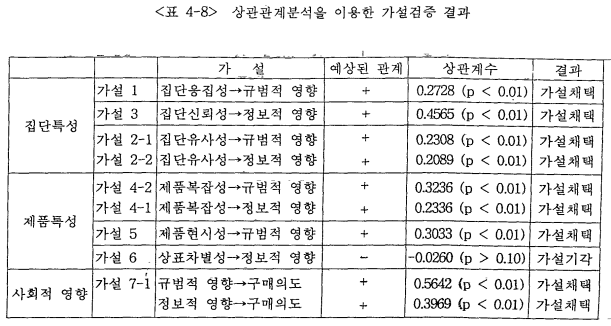

2. 공변량 구조모형분석(LISREL)에 의한 가설검증
LISREL은 종래의 회귀분석 또는 경로분석에서 요구되던 비현실적인 가정을 버리고 보다 현실적인 상황에서의 분석을 가능하게 해 준다는 점에서 최근 그 사용이 증가하고 있는 분석기법이다. LISREL에서는 요인분석과 경로분석을 결합함으로서 연구의 이론변수가 여러 개의 측정변수를 가지고 있는 공통적인 부분에 의해 반영되게 하는 한편, 이들 이론변수와 관계가 없는 측정변수 고유의 부분(오차)을 모형 내에서 허용하고 있다. 본 연구에서도 LISREL을 이용하여 설정한 모델의 적합도와 가설검증을 실시해 보고자 한다.
먼저 LISREL을 사용하기 위해서는 표본의 크기, 연구모형의 확인가능성, 연구자료의 다변량 정규분포가능성 등에 대한 검토가 필요하다. LISREL적용을 위한 연구표본의 크기에 대해서는 여러 가지 주장들이 제기되고 있는데, 일반적으로 표본수가 최소한 100개 이상(김재일 1989, p.91.)이면서 가능하면 200개 이상(Boomsma 1982)이 바람직하고, 최우추정법(ML)을 사용할 경우에는 표본의 크기에서 자유도를 차감한 수가 50이상 되어야 한다고 한다(Bagozzi 1991). 본 실증분석에서 사용된 334개의 표본수는 이러한 기준을 모두 만족시키고 있으므로 연구표본 크기에 대한 LISREL의 전제조건에는 문제가 없다고 판단된다.
LISREL에서 전반적인 모형의 적합도를 판단하는 기준으로는 χ2값의 유의도, GFI, AGFI, RMR 등이 많이 사용된다(Bagozzi and Yi 1988). χ2값이 유의적이면, 적합도가 좋지 않고, 유의적이지 않으면 적합도가 좋다. χ2값이 작고 유의적이지 않다는 것은 모형과 표본자료간에 아주 밀접한 상관관계가 있다는 것을 의미한다. 그리고 다른 적합도로서 GFI, AGFI 및 RMR의 적합도가 제시되고 있는데, 대체적으로 GFI와 AGFI는 0.9를 넘어서야 하고, RMR은 0.05보다 작아야 적합도가 있다고 판단된다. 본 연구에서는 LISREL에서 기본적으로 제공하는 χ2값, GFI, AGFI 및 RMR을 중심으로 전반적 적합도를 평가하였다.
또한 연구모형의 확인가능성은 측정하려는 특징수(parameter)가 LISREL식 내에서 계산이 가능한가를 의미하는데, 이의 기준으로서는 "사용되는 정보의 수가 최소한 추정하려는 미지수보다 많아야 한다"이다.6) 본 연구에서 분석한 각 하위모형은 이러한 기준을 만족시키고 있다.
마지막으로 최우추정법(ML)을 사용하는 경우에는 특히 자료가 다변량 정규분포(multivariate normal distribution)를 이룬다는 가정이 충족되어야 한다. LISREL에서는 표본의 다변량 정규분포의 검정을 PRELIS라는 프로그램을 통해서 수행할 수 있게 하였다. 본 연구에서 사용된 334개의 표본자료를 평가해 본 결과 문제가 될 만한 분포상의 특징이 확인되지 않았으며, PRELIS에서 제공하고 있는 다변량 정규분포의 평가지표인 관련 다변량첨도수치(Relative Multivariate Kurtosis)7) 에서도 1.023을 나타내어 연구자료가 다변량 정규분포 가정을 크게 위반하지 않는 것으로 나타났다.
본 연구에서는 가설검증을 위해 LISREL PC VERSION 7.13을 사용하였으며 입력자료는 변수들간의 상관관계 행렬을 사용했고 최우추정법(ML)을 통해 특징수들을 추정하였다.
1) 집단 및 제품 특성과 사회적 영향간의 하위모델 1
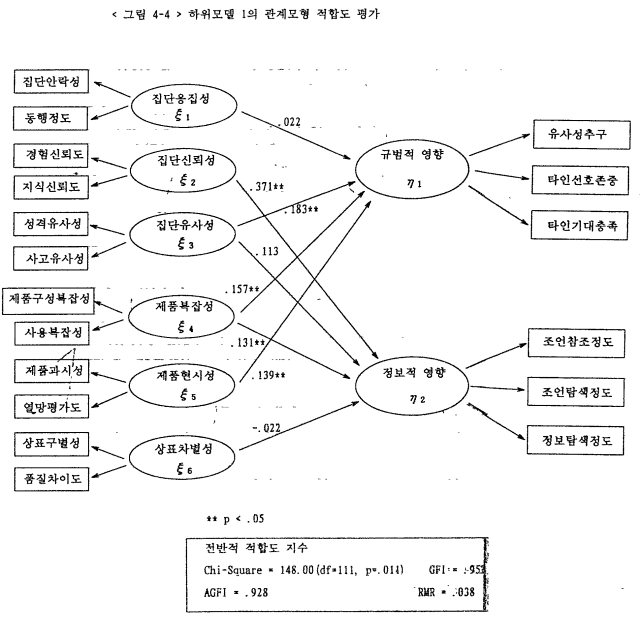
집단 및 제품 특성과 사회적 영향간의 관계모형의 적합도는 < 그림 4-4 > 에 나타나 있다. 전반적 적합도 지수를 보면 χ2의 p값이 0.011로 나타났으나, GFI와 AGFI가 0.9이상으로 나왔고 RMR도 0.05이하로 나타나, 연구모형과 실제자료가 비교적 일치되고 있음을 보여주고 있다.
한편 하위모델 1에서 얻어진 특징수들의 추정치와 표준오차, t값들은 < 표 4-9 >에 나타나 있다. 본 연구의 연구가설들인 변수들 간의 관계는 γ계수에 나타나고 있다. 이를 토대로 가설검증 결과를 살펴보면 다음과 같다.
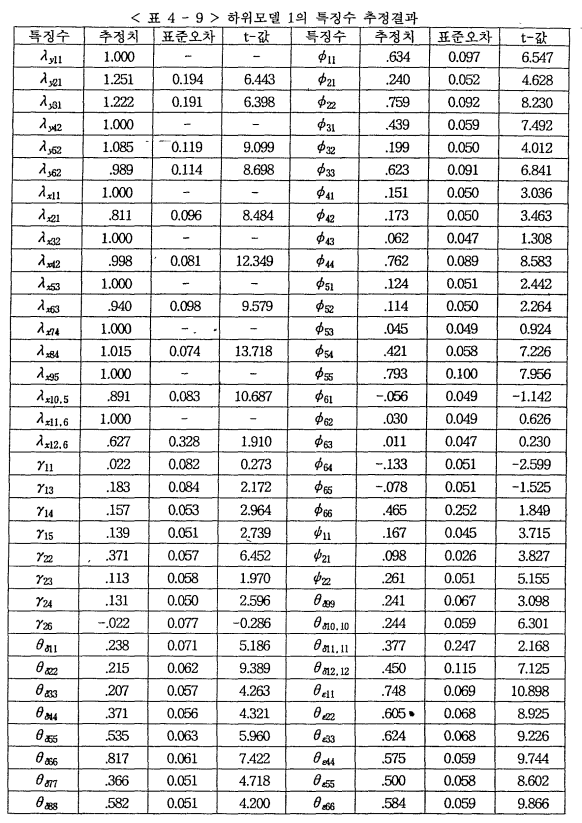
먼저 집단응집성이 높을수록 규범적 영향이 클 것이라는 가설 1은 지지되고 있지 않다(γ11=0.022, t= 0.27
. 이 결과는 앞의 상관관계 분석과 일치하고 있지 않다. 집단유사성이 높을수록 규범적 영향이 클 것이라는 가설 2-1은 지지되고 있다(γ13=0.183, t=2.172). 이는 앞의 상관관계 분석과 일치하고 있다. 집단유사성이 높을수록 정보적 영향이 클 것이라는 가설 2-2는 지지되고 있지 않다(γ23=0.113, t=1.970). 이는 앞의 상관관계분석과 일치하고 있지 않다. 집단신뢰성이 높을수록 정보적 영향이 클 것이라는 가설 3은 지지되고 있다(γ22=0.371, t=6.452). 이는 앞의 상관관계 분석의 결과와 일치한다. 제품복잡성이 클수록 규범적 영향이 클 것이라는 가설 4-1은 지지되고 있으며(γ14=0.157, t=2.964), 정보적 영향도 클 것이라는 가설 4-2도 지지되고 있다(γ24=0.131, t=2.596). 이는 앞의 상관관계분석의 결과와 일치한다. 제품현시성이 높을수록 규범적 영향이 클 것이라는 가설 5는 지지되고 있다(γ15=0.139, t=2.739). 이는 앞의 상관관계분석과 일치한다. 상표차별성이 낮을수록 정보적 영향이 클 것이라는 가설 6은 기각되고 있다(γ26=-0.022, t=-0.286). 이는 앞의 상관관계분석의 결과와 일치한다.
종합해보면 집단유사성, 제품복잡성, 제품현시성은 규범적 영향에 영향을 미치고 집단신뢰성, 제품복잡성은 정보적 영향에 영향을 미친다는 것을 하위모델 1을 통해서 알 수 있다.
2) 사회적 영향과 구매의도간의 하위모델 2
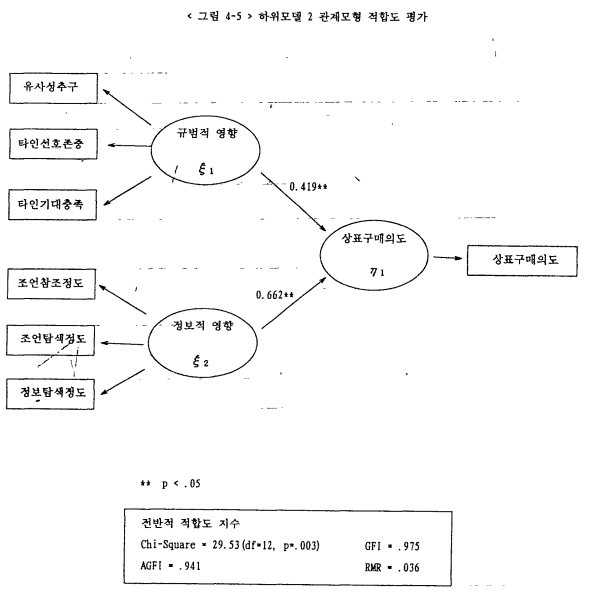
사회적 영향과 구매의도 간의 관계모형의 적합도는 < 그림 4-5 > 에 나타나 있다. 전반적 적합도 지수를 보면 χ2의 p값이 0.003으로 나타났으나, GFI, AGFI가 0.9이상으로 나왔고 RMR도 0.05이하로 나타나, 연구모형과 실제자료가 비교적 일치되고 있음을 보여주고 있다.
한편 하위모델 1에서 얻어진 특징수들의 추정치와 표준오차, t값들은 <표 4-10>에 나타나 있다. 본 연구의 연구가설들인 변수들 간의 관계는 γ계수에 나타나고 있다. 이를 토대로 가설검증 결과를 살펴보면 다음과 같다.
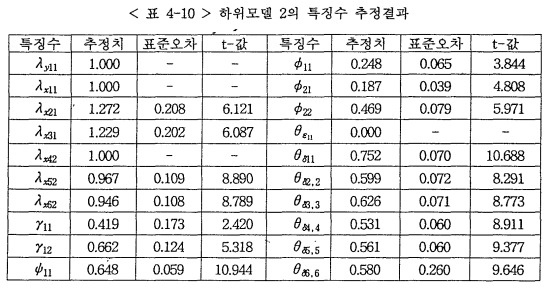
규범적 영향과 정보적 영향이 구매의도에 영향을 미칠 것이라는 가설 7-1은 지지되고 있다(γ11=0.662, t=2.420; γ12=0.662, t=5.318). 이는 앞의 상관관계분석의 결과와 일치하고 있다.
이번에는 ATSCI의 고저에 따른 사회적 영향과 구매의도간의 관계에 대한 가설 7-2를 검증하기 위해서 표본을 ATSCI고저에 따라 두 집단으로 나누어 하위모델 2를 검토해 보았다.
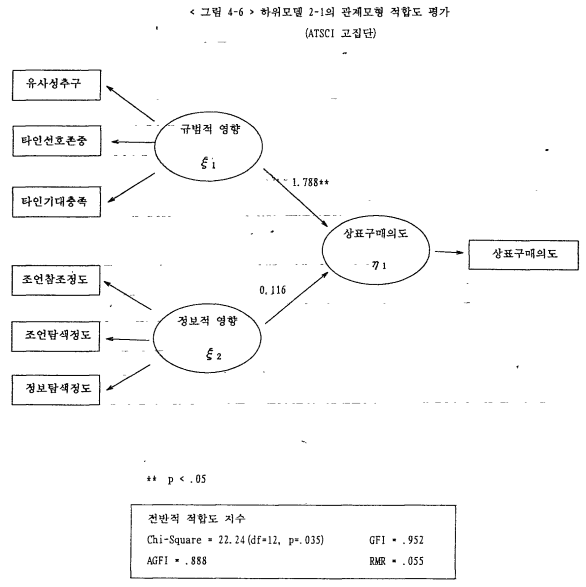
먼저 ATSCI가 높은 집단을 대상으로 한 하위모델 2-1의 적합도는 < 그림 4-6>에 나타나 있다. 전반적 적합도 지수를 보면 chi^2 =22.24(df=12, p=0.035)로 나타났고 GFI=.952, AGFI=.888, RMR=0.055로서 모델의 부합도가 약간 떨어지는 것으로 나타났다. 하위모델 2-1에서 얻어진 특징수들의 추정치와 표준오차, t값들은 < 표 4-11 >에 나타나 있다. 이 모델에서는 상표구매의도에 규범적 영향이 큰 것으로 나타나고 있으며(γ11=1.788, t=2.817), 정보적 영향은 미미한 것으로 나타나고 있다(γ12=0.116, t=0.433). 따라서 이는 가설 7-2를 지지하고 있다.