
2. Pearson 상관관계분석
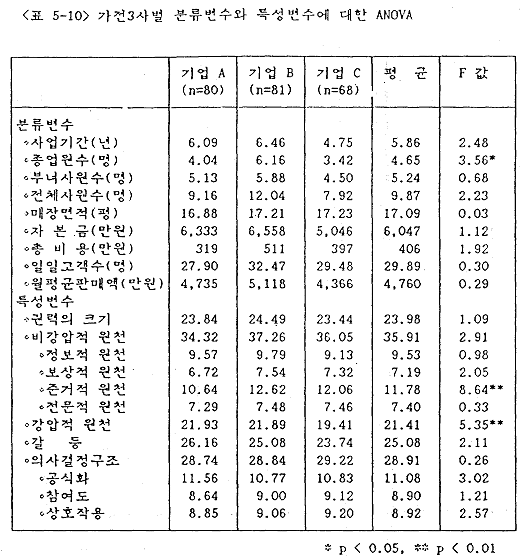
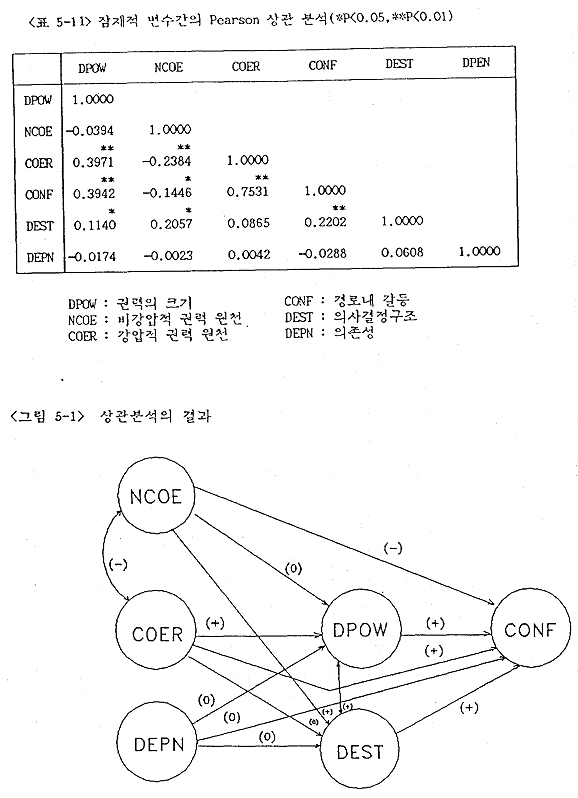
Pearson 상관분석을 실시하여 여섯 가지 구성개념 사이의 연관성을 개괄적으로 살펴 보았다. 그 결과 <표 5-11>에서 보는 바와 같이 강압적 권력원천-권력, 갈등-비강압적 권력원천, 갈등-강압적 권력원천, 의사결정구조-비강압적 권력원천, 권력-의사결정구조, 갈등-권력, 갈등-의사결정구조 사이에 유의적 연관성을 보였다. 이들 결과를 연구모형에 표시하면 다음과 같다(<그림 5-1> 참조).
3. 중회귀 분석
상관분석에서는 하나의 변수와 하나의 변수 사이에 나타나는 연관성을 살펴보았으나, 이번에는 2개 이상의 독립변수가 하나의 종속변수와 어떠한 연관성을 갖는지를 살펴보기로 한다. 모형에 따른 검증식은 다음과 같이 표시할 수 있다.
① DPOW = f(NCOE, COER, DEPN)
② DEST = f(NCOE, COER, DEPN)
③ CONF = f(NCOE, COER, DEPN)
DPOW : 권력의 크기
NCOE : 비강압적 권력원천
DEST : 의사결정구조
COER : 강압적 권력원천
DEST : 의사결정구조
COER : 강압적 권력원천
CONF : 갈등
DEPN : 의존성
중회귀분석을 실시하기 위해서는 몇 가지 기본적인 가정을 검토하여야 하는데, 선형성(linearity)·동일분산(equal variance)·오차항의 독립성(independence of error)·정규성(normality)·다중공선성(multicollinearity)의 문제를 살펴 보아야 한다.14) 본 연구에서도 분석할 자료들이 이들 여러 가정들을 충족시키고 있는지를 먼저 살펴보고 각 모형에 대한 중회귀분석을 하였다.
1) 권력의 원인변수로서 권력원천과 의존성
권력의 원천(강압적 원천·비강압적 원천)과 의존성이 권력의 크기를 결정하는 요인인지를 알기 위해 회귀분석을 하였다. 회귀분석을 하기에 앞서 회귀분석의 기본가정을 충족시키는지의 여부를 살펴 보았다.
먼저 선형성과 동일분산의 조건을 충족시키는지를 알기 위해 표준화된 선포도(scatterplot)를 작성하여 보았더니 잔차(residuals)가 균등하게 분포되어 이들 가정을 충족하였다. 오차항의 독립성 유무는 Durbin-Watson test를 통해 검증하였는데, 값이 1.54로서 α=0.01, k=3, n=208의 임계치인 1.48~1.60에 포함되어 계열상관(serial correlation)은 없다고 볼 수 있다. 정규성의 가정을 검토하기 위해서 각 변수들에 대해 normality probability plot(P-P plot)을 작성하여 보니 정규 분포를 벗어나지 않았다. 마지막으로 독립변수간의 다중공선성 여부를 확인하기 위해 상관계수를 살펴보았더니 그 값이 0.013~0.238로 독립변수들간의 독립성이 보장되었다고 볼 수 있으며, 변수의 선택도 단계별 방법(stepwise method)를 지정하였다.
회귀분석의 모든 가정을 충족하고 있기에 권력을 종속변수로 하고, 비강압적 원천·강압적 원천·의존성 등을 독립변수로 회귀분석을 한 결과는 <표 5-12>와 같다. 이를 보면 강압적 권력원천만이 권력의 크기에 유의적인 정(+)의 영향을 미쳤다. 그리고 결정계수 R2-17.35%이고, F값은 43.24로서 회귀식이 통계적으로 유의하였다.( P< 0.01)

2) 의사결정구조의 원천변수로서 권력원천과 의존성
권력의 원천(강압적 원천·비강압적 원천)과 의존성이 의사결정구조와 어떤 연관성을 갖는지를 알기 위해 회귀분석을 실시하였다. 회귀분석을 하기에 앞서 회귀분석의 기본가정을 충족시키는지의 여부를 살펴 보았다.
먼저 선형성과 동일분산의 조건을 충족시키는지를 알기 위해 표준화된 산포도(scatterplot)를 작성하여 보았더니 잔차가 균등하게 분포되어 이들 가정을 충족하였다. 오차항의 독립성 유무는 Durbin-Watson test를 통해 검증하였는데, 값이 1.76으로서 α= 0.01, k=3, n=229의 임계치인 1.48~1.60에 포함되지 않았다. 이는 임계치의 상한값보다 크지만 α=0.05일때의 임계치는 1.61~1.74이므로 오차항이 약간의 정(+)의 관련을 갖는 것으로 볼 수 있으나, 큰 문제는 되지 않는다고 판단된다. 정규성의 가정을 검토하기 위해서 각 변수들에 대해 normality probability plot(P-P plot)을 작성하여 보니 정규분포를 벗아나지 않았다. 마지막으로 독립변수들간의 다중공선성 여부를 확인하기 위해 상관계수를 살펴 보았더니 그 값이 0.019~0.245로 독립변수들간의 독립성이 보장되었다고 볼 수 있다.
회귀분석의 모든 가정을 충족하고 있기에 의사결정구조를 종속변수로 하고, 비강압적 원천·강압적 원천·의존성 등을 독립변수로 하여 회귀분석을 한 결과는 <표 5-13>과 같다. 이를 보면 비강압적 원천과 강압적 권력원천이 의사결정구조에 정(+)의 영향을 미쳤다. 그리고 결정계수 R2=3.4%로 직극히 적은 값이었으나, F값은 7.30으로서 회귀식이 통계적으로 유의하였다.( P< 0.05).

3) 갈등의 원인변수로서 권력원천과 의존성
권력의 원천(강압적 원천·비강압적 원천)과 의존성이 경로내 갈등과 어떤 연관을 갖는지를 알기 위해 회귀분석을 실시하였다. 회귀분석을 하기에 앞서 회귀분석의 기본가정을 충족시키는지의 여부를 살펴 보았다. 먼저 선형성과 동일분산의 조건을 충족시키는지를 알기 위해 표준화된 산포도(scatterplot)로 작성하여 보았더니 잔차가 균등하게 분포되어 이들 가정을 충족하였다. 오차항의 독립성의 유무는 Durbin-Watson tent를 통해 검증하였는데, 값이 1.70으로서 α= 0.01, k=3, n=229의 임계치인 1.48~1.60에 포함되지 않았다. 그러나 α=0.05이면 임계치가 1.61~1.74이기 때문에 임계치에 포함된다. 이를 통해 약간의 계열상관이 있다고 볼 수 있으나 큰 문제는 없다고 판단된다. 정규성의 가정을 검토하기 위해 각 변수들에 대해 normality probability plot(P-P plot)을 작성하여 보니 정규분포를 벗어나지 않았다. 마지막으로 독립변수들간의 다중공선성 여부를 확인하기 위해 상관계수를 살펴 보았더니 그 값이 0.014~0.266으로 독립변수들간의 독립성이 보장되었다고 할 수 있다.
회귀분석의 모든 가정을 충족하고 있기에 갈등을 종속변수로 하고, 비강압적 원천·강압적 원천·의존성 등을 독립변수로하여 회귀분석을 한 결과는 <표 5-14>와 같다. 이를 보면 강압적 원천이 경로내 갈등에 정(+)의 영향을 미쳤다. 그리고 결정계수 R2=56.6%로 설명력이 괜찮았으며, F값은 257.08로서 회귀식이 통계적으로 유의하였다.(P<0.01)


기금까지 세 가지 중회귀분석의 결과를 보면 앞의 상관분석과 비슷한 결과도 있으나 약간 다르기도 하다. 즉 권력의 크기와 강압적 권력원천, 의사결정구조와 비강압적 권력원천, 경로내 갈등과 강압적 권력은 같은 결과이다. 그러나 상관분석에서는 의사결정구조와 비강압적 원천만이 유의적이었으나 회귀분석에서는 의사결정구조와 2가지 권력원천이 모두 유의적이었다. 또한 상관분석에서는 갈등과 2가지 권력원천이 모두 유의적이었으나 회귀분석에서는 갈등과 강압적 원천만이 유의적이었다(<표 5-15> 참조). 이와 같이 차이가 나는 이유는 상관분석이 하나의 변수와 하나의 변수사이의 연관성을 보는 것임에 비해, 중회귀분석은 2개 이상의 독립변수를 동시에 고려하게 되고 이들 독립변수들이 서로 완전한 독립성을 갖지 않았기 때문이다.
다만 의존성 변수가 어디에도 연관성을 보이지 않는 것은 가전3사 대리점들이 본사에 대한 의존도가 절대적으로 높기 때문에 유의적인 차이를 보이지 않는 것으로 판단된다. 즉, 설무에 응한 229개 대리점들의 본사에 대한 평균의존도는 93.97%이었으며, 표준편차는 10.36%로서 권력·의사결정구조·갈등에 대해 유의적인 차이를 나타내지 않았다.
4. 정준상관분석
앞의 중회귀분석에서는 2개 이상의 독립변수가 하나의 종속변수에 영향을 미친다는 것을 전제로하여 회귀식을 구성하여 연관성을 검증하였다. 그런데 본 연구에서는 각각의 구성개념을 두 가지 이상의 차원으로 측정하였기 때문에 독립변수군과 종속변수군이 형성되어 이들 변수군간의 연관성 분석은 정준상관분석(canonical correlation analysis)을 통해 검증하도록 하였다.
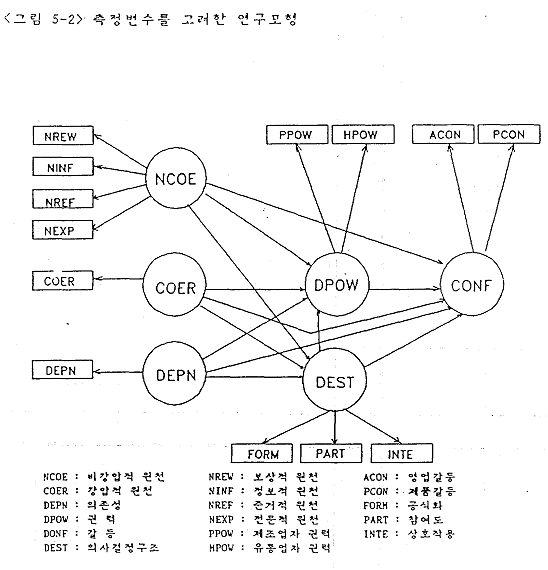
정준상관분석을 하기 위한 연구모형은 다음의 <그림 5-2>와 같이 표시할 수 있으며, 이를 식으로 표현하면 다음과 같은 아홉 가지의 식이 도출된다.
① (DPOW, MPOW) = f(NREW, NINF, NREF, NEXP)
② (ACON, PCON) = f(NREW, NINF, NREF, NEXP)
③ (FORM, PART, INTE) = f(NREW, NINF, NREF, NEXP)
④ (PPOW, MPOW) = f(FORM, PART, INTE)
⑤ (ACON, PCON) = f(PPOW, MPOW)
⑥ (ACON, PCON) = f(FORM, PART, INTE)
⑦ (PPOW, MPOW) = f(NREW, NINF, NREF, NEXP, COER)
⑧ (FORM, PART, INTE) = f(NREW, NINF, NREF, NEXP, COER)
⑨ (ACON, PCON) = f(NREW, NINF, NREF, NEXP, COER)
의존선 변수는 앞의 상관 분석과 회귀분석을 통해 전혀 유의적이지 못했기에 정준상관분석에서는 제외하였다.
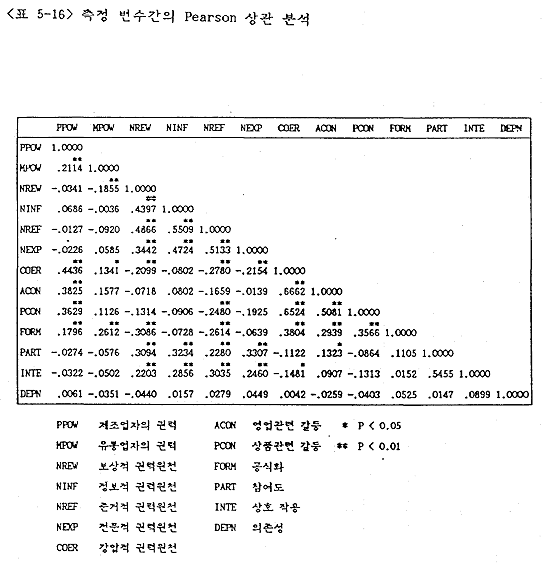
분석에 이용할 13가지 측정변수들의 개관적인 관련성을 알기 위해 상관분석을 한 결과는 <표 정5-16>과 같다.
정준상관분석은 SPSS PC +에서는 MANOVA에 의해 처리되기 때문에 본 연구도 이를 이용하였다. 다변량분산분석(multivariate analysis of variance)을 하기 위해서는 (1) 변수들이 다변량 정규분포(multivariate normal distribution)을 이루어야 하며, (2) 종속변수들을 구분하여 주는 집단들이 동일한 분산-공분산 행렬(variance-covariance matrix)를 갖고 있어야 한다. 또한 종속변수들이 상관관계가 없으면 처음부터 다변량 분석이 불필요하므로 종속변수들에 대한 독립성 여부도 검토하여야 한다.15)
본 연구에서는 각 변수군들끼리의 관련성을 아홉 가지 모형으로 나누어 각 모형의 유의성을 검증하려 한다. 모형의 검증에 앞서 자료들이 다변량분산분석을 할만한 가치가 있는지를 알기 위해 Bartlett's test of sphericity를 통해 종속변수들이 전부 독립적이라는 귀무가설을 기각할 수 있기에 ( P< 0.01) MANOVA를 실시해도 무방하다 판단하였다.
독립변수가 연속성 변수이기 때문에 집단간의 분산-공분산 행렬의 동일성 여부에 대한 검증은 불필요 하였다. 그리고 각 변수들의 정규성 여부는 각 변수들에 대한 normal probability plot과 stem-and plot을 통해 확인하였는데 정규분포에서 크게 벗아나지 않은 것으로 판단되었다.
정준상관분석을 통해 얻은 canonical function을 해석하기 전에 함수의 통계적 유의성, canonical correlation의 크기, redundancy index 등을 살펴 보는 것이 필요하다.16)
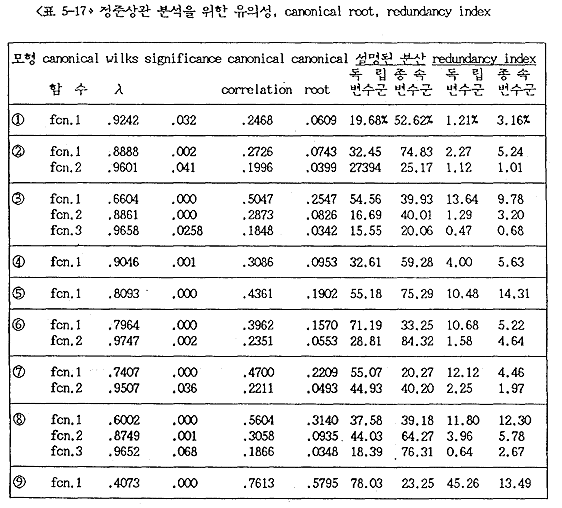
다음의 <표 5-17>에서 보는 바와 같이 아홉 가지 모형에 대한 정준상관분석을 하기 위해 도출된 canonical 함수들은 통계적으로 유의하였다. 반면에 canonical correlation17) canonical root18), 설명된 분산19), 그리고 redundancy index20)를 보면 별로 만족스럽지 못하다. 그러나 본 연구의 분석에 이용되어지는 자료가 비율척도에 의해 구한 것이 아니며 다만 변수 사이에 관련성 유무를 파악하는 것이 그 목적이므로 해석하는데는 큰 무리가 없다고 판단된다. 다음에 canonical 함수를 해석하는데 있어서 canonical weight를 이용할지, 또는 canonical liading을21) 이용할지에 대한 문제이다. 전통적으로는 canonical weight를 보고 해석하였으나 변수들 사이에 다중공선성이 있으면 값이 작아지며, 표본에 따라 극히 불안정(instability)하기 때문에 요즈음은 canonical loading이 많이 이용된다22). 따라서 본 연구에서는 canonical loading을 통해 결과를 해석하려 한다.
1) 비강압적 권력원천과 권력
비강압적 권력원천인 보상적 원천·정보적 원천·준거적 원천·전문적 원천 등의 독립변수군이 제조업자의 권력과 유통업자의 권력이라는 종속변수군과 이러한 연관이 있는지를 분석하였다. 그 결과 보상적 권력원천을 적게 행사할수록 유통업자는 스스로 권력을 많이 갖고 있다고 지각하였다.
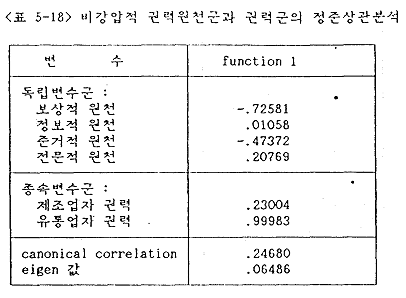
2) 비강압적 권력원천과 경로내 갈등
비강압적 권력원천·전문적 원천 등의 독립변수군의 영업갈등과 상품갈등이라는 종속변수군과 어떠한 연관이 있는지를 분석하였다. 그 결과 준거적 권력원천이 적게 행사될수록 영업관련 갈등과 제품관련 갈등이 높아졌다(함수 1). 또한 전문적 원천을 많이 제공할수록 영업관련 갈등은 줄어든다(함수 2).
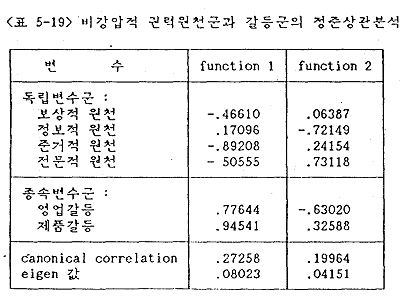
3) 비강압적 권력원천과 의사결정구조
비강압적 권력원천인 보상적 원천·정보적 원천·준거적 원천·전문적 원천 등의 독립변수군이 공식화·참여도·상호작용이라는 종속변수군과 어떠한 연관이 있는지를 분석하였다. 그 결과 보상적 원천·정보적 원천·준거적 원천이 적을수록 공식화는 높아지며, 참여도와 상호작용은 적었다(함수 1). 전문적 원천이 많을수록 공식화가 높아지고 참여도가 많아졌다(함수 2).
다음 페이지로