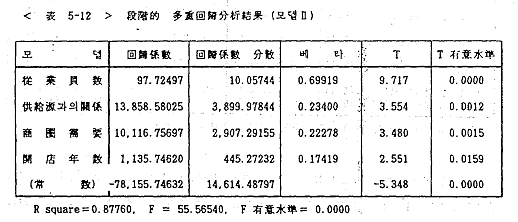
<표 5-12>에 있는 회귀분석모델II는 종업원수, 공급원과의 관계, 상권수요, 개점연수로 구성되어 있는데 R square = 0.87760으로 88%의 높은 설명력을 보이고 있는데, 회귀방정식의 F 검증은 매우 유의(유의수준 = 0.0000)하게 나타나 모델의 검증력은 매우 높음을 알 수 있다.

다음으로 회귀방정식에 포함된 변수들의 회귀계수에 대한 T검증을 보면 종업원수는 0%에 가까운 수준으로 유의적인 정의 관계를 보여주고 있고, 공급원과의 관계와 상권수요는 0.1%수준으로 유의적인 정의 관게를 개점연수는 1.59% 수준으로 유의적인 정의 관계를 보여주고 있다.

변수간의 설명력을 보면 종업원수, 공급원과의 관계, 상권수요, 개점연수의 순으로 나타나고 있다. 이를 회귀방정식으로 나타내면 다음과 같다.

매출액 = 97.72497 ×종업원수 + 13,858.58025 ×공급원과의 관계 + 10,116.75697 ×상권수요 + 1,135.74620 ×개점연수 - 78,155.74632

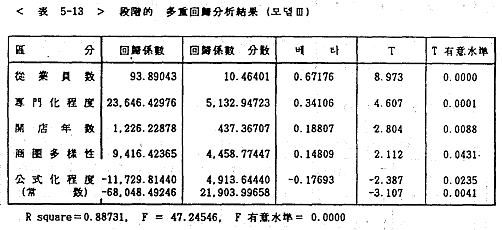
<표 5-13>에 있는 회귀분석모델III은 종업원수, 전문화정도, 개점연수, 상권다양성, 공식화정도로 구성되어 있는데 R square=0.88731로 89%의 높은 설명력을 보이고 있으며, 회귀방정식의 F검증은 매우 유의(유의수준=0.0000)하게 나타나 모델의 검증력은 매우 높음을 알 수 있다.

다음으로 회귀방정식에 포함된 변수들의 회귀계수에 대한 T검증을 보면 종업원수와 전문화정도는 0%에 가까운 수준으로 유의적인 정의 관계를 보여주고 있고, 개점연수는 0.88% 수준으로, 상권다양성은 4.3%수준으로 유의적인 정의 상관관계를 보여주고 있고, 공식화정도는 모델I에서와 마찬가지로 2.35%의 유의수준으로 부의 상관관계를 보여주고 있다. 변수간의 설명력을 보면 종업원수, 전문화정도, 개점연수, 공식화정도, 상권다양성의 순으로 나타나고 있다. 이를 회귀방정식으로 나타내면 다음과 같다.

매출액 = 93.89043 ×종업원수 + 23,646.42976 ×전문화정도 + 1,226.22878 ×개점연수 + 9,416.42365 ×상권다양성 - 11,729,81440 ×공식화정도 - 68,048,49246

<표 5-14>에서 모델 IV를 보면 상권다양성, 공급원과의 관계, 종업원수, PB상품구성비율로 이루어져 있는데 R square=0.85538로 86%의 설명력을 보이고 있다. 회귀방정식의 F검증은 매우 유의하게 나타나 모델의 검증력은 매우 높음을 알 수 있다. 다음으로 회귀방정식에 포함된 변수들의 회귀계수에 대한 T검증을 보면 종업원수는 0%, 상권다양성과 공급원과의 관계는 각각 9.4%와 0.84%의 유의수준으로 정의 관계를 보여 주고 있고, PB상품구성비율은 9%의 유의수준으로 부의 관계를 보여 주고 있어 단순회귀분석에서 기각되었던 가설과는 정반대로 매출액에 부의 영향을 미치고 있음을 보여 주고 있다.

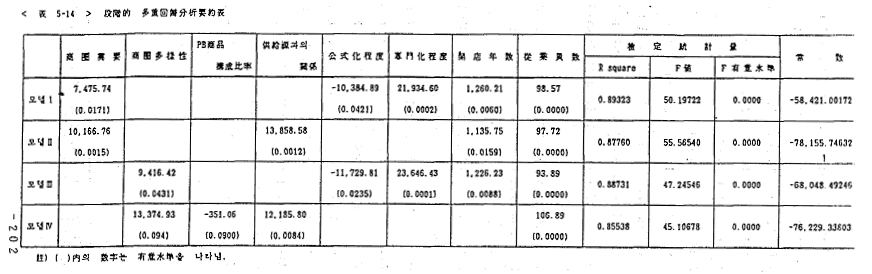
<표 5-14>에서 보는 바와 같이 상권수요, 상권다양성, 공급원과의 관계, 전문화정도, 개점연수, 종업원수는 연구가설을 더욱 뒷받침해 주고 있으며, PB상품구성비율과 공식화정도는 연구가설과는 정반대로 매출액에 영향을 미치고 있음을 알 수 있다. 그 외에 상권지리, 이미지, 직영율, 서비스, 분위기, 집권화정도, 그룹소속유무, 매장면적, 임직원자질, 신용카드회원수, 총신용판매비율은 단순회귀분석결과 이외에는 더 이상 연구가설을 기대하는 증거를 찾을 수 없었다.

다음으로 회귀분석의 가정을 검증해 보기 위해 잔차(residuals)를 분석해 보도록 한다. 회귀모델은 선형모델, 오차항간의 체계적인 관련성(serial correlation of error, autocorrelation), 잔차의 정규분포(normality), 오차항분산의 동질성(honoscedasticity, equal variance of error), 다중공선성의 무(nonmulticollinearity) 등의 기본적인 가정을 가지고 있다.¹²⁾

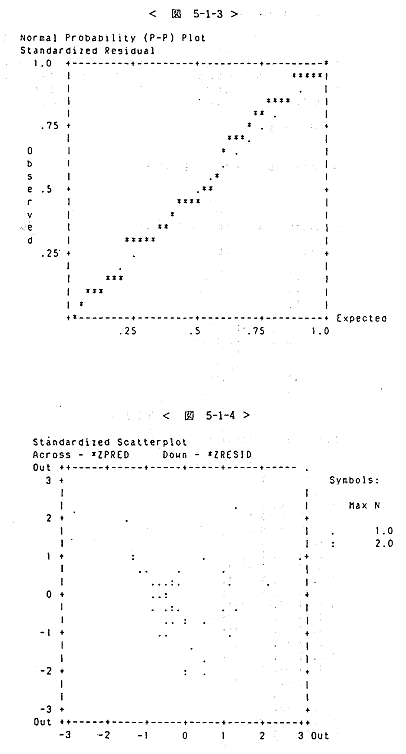
먼저 모델I에 대해서 보면 공식화정도와 전문화정도, 전문화정도와 종업원수, 개점연수와 종업원수간에 각각 0.54, 0.40, 0.36의 상관관계를 보이고 있으므로 이들 간의 다중공선성(multicollinearity) 가능성이 높으므로(<표 5-15>) 해석상의 주의를 요한다. 오차액의 분석에 있어서는 오차액을 표준화한 *ZRESID에서 평균이 0이며 표준편차가 1이어야 하는데 표준편차가 1.3790으로 약간 크게 나타나고 있어 분포가 중심부분에서 약간 퍼져 있음을 알 수 있으며 이를 그림으로 나타낸 것이 <도 5-12>의 히스토그램이다. 오차항간의 계열상담(serial correlation)을 검증하는 Durbin-Watson 통계량의 경우 2.17045로 나타났는데 이는 유의수준 0.05, 독립변수 수 5개, 표본수 45를 D-W 표에서 찾아보면 D-W=<1.29, 1.78>이 임계치이므로 자기상관 제로의 가설을 채택함을 알 수 있다. 오차액 분산의 동질성(honoscedasticity)을 알아 보기 위해 종속변수의 크기와 오차의 분산을 나타내 준 결과 <도 5-1-4>의 Scatterplot을 보면 예측치(ZPRED)가 커져도 오차(ZRESID)의 분산이 커지거나 적어지지 않는 분포를 이루고 있어 오차항의 분산은 동질적인 것으로 판단된다.

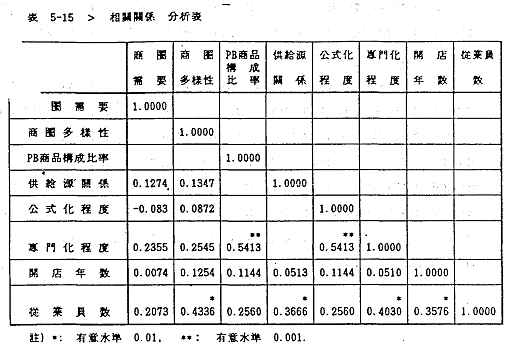
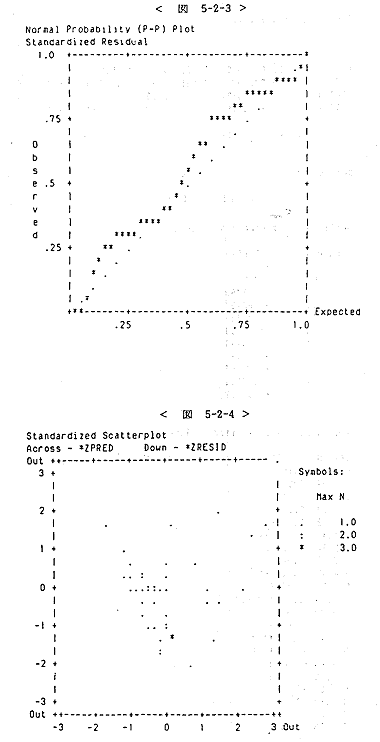
모델II에 대해서 보면 종업원수가 공급원과의 관계, 개점연수와 각각 0.37, 0.36의 상관관계를 보이고 있다(<표 5-15>). 오차항의 분석에 있어서는 오차항을 표준화한 *ZRESID에서 표준편차가 1.3419로 1보다 크게 나타나 분포가 중심부분에서 약간 퍼져 있음을 알 수 있다(<도 5-2-2>). 오차항간의 계열상관을 검증하는 D-W 값이 2.05506으로 나타나 D-W 통계량(유의수준 0.05, 독립변수 수 4개, 표본수 45개)의 임계치 <1.34, 1.72)와 비교해 보면 자기상관제로의 가설을 채택하고 있다. 오차항 분산도 0을 중심으로 고루 분포되고 있어 동질적인 것으로 판단된다(<도 5-2-4>).

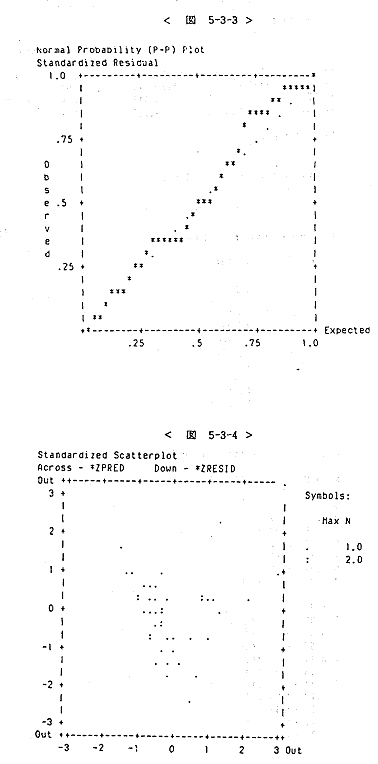
모델III에 대해서 보면 공식화정도와 전문화정도, 종업원수와 상권다양성ㆍ전문화정도ㆍ개점연수와 상당한 상관관계를 보이고 있다(<표 5-15>). 오차항의 분석에 있어서는 오차항을 표준화한 *ZRESID에서 표준편차가 1.3388로 1보다 크게 나타나 분포가 중심부분에서 약간 퍼져 있음을 알 수 있다(<도 5-3-2>). 오차항간의 계열상관을 검증하는 D-W 값이 2.10873으로 나타나 D-W 통계량(유의수준 0.05, 독립변수 수 5개, 표본수 45개)의 임계치<1.29, 1.78>와 비교해 보면 자기상관 제로의 가설을 채택함을 알 수 있다. 오차항 분산도 0을 중심으로 고루 분포하고 있어 동질적인 것으로 판단된다(<도 5-3-4>).

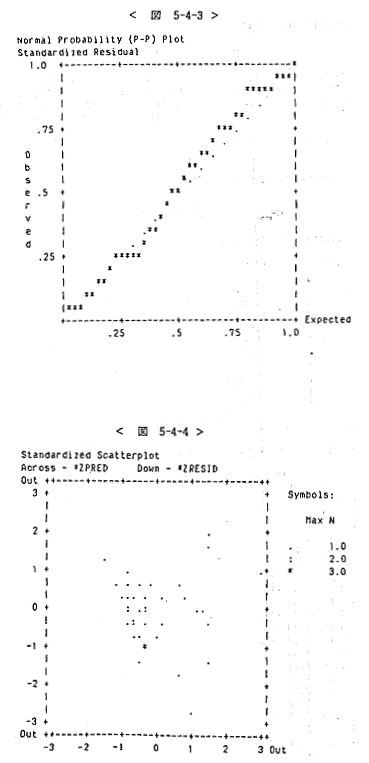
모델IV에 대해서 보면 종업원수가 상권다양성과 상당한 상관관계를 보이고 있다(<표 5-15>). 오차항의 분석에 있어서는 오차항을 표준화한 *ZRESID에서 표준편차가 0.9349로 1보다 약간 작게 나타나 분포의 중심부분에 약간 몰린 분포를 이루고 있음을 알 수 있다(<도 5-4-2>). 오차항간의 계열상관을 검증하는 D-W 값이 1.92565로 나타나 D-W 통계량(유의수준 0.05, 독립변수 수4개, 표본수 45개)의 임계치<1.34, 1.72>와 비교해 보면 자기상관 제로의 가설을 채택함을 알 수 있다. 오차항 분산도 0을 중심으로 고루 분포되고 있어 동질적인 것으로 판단된다(<도 5-4-4>).

3. 요인점수를 이용한 회귀분석

제5장 2절의 타당성검사에서 사용하였던 주성분분석(principal components analysis)을 이용하여 다음의 회귀분석을 용역하게 하고 소수의 새로운 변수로 축소키기기 위해 배리맥스 직각회전시켜 아이겐치 1 이상을 기준으로 요인 5개만을 선정한 결과 누적분산은 69.8%로 요인들의 설명력을 나타내 주고 있다.

요인분석후 요인점수(factor score)를 구하여 다음의 회귀분석에 이용하고자 한다. 이는 본 연구의 경우 변수들의 수가 너무 많아 변수들간의 다중공선성(multicollinearity)이 높아 사용하려고 하며, 요인점수는 요인점수계수행렬(factor score coefficient matrix)을 이용하여 구한다.

요인점수를 이용하여 회귀분석한 결과가 <표 5-16>에 요약되어 있다.

R square=0.84187로 비교적 높은 84%의 설명력(explanatory power)을 보이고 있으며, 회귀방정식의 F검증은 매우 유의(유의수준=0.0000)한 것으로 나타났다. 요인들의 회귀계수에 대한 T검증을 보면 요인 4만 13% 수준으로 유의적인 정의 관계를 보이고 있고, 나머지 요인 4개는 0%에 가까운 유의수준을 보이고 있다.

요인간의 설명력을 보면 요인2, 요인1, 요인5, 요인3, 요인4의 순서로 나타나고 있다. 여기서 요인2는 PB상품비율, 매장면적, 직영율이 높은 부하가 걸려 있어 점포의 영업전략을 나타내며, 요인 1은 그룹소속유무, 이미지, 종업원수, 공급원과의 관계, 분위기, 임직원자질, 공식화정도, 전문화정도, 집권화정도, 자사신용카드회원수, 신용판매비율이 높은 부하가 걸려 있어 점포의 특성을 반영하고 있으며, 요인 5는 상권지리, 신용판매비율을 비롯해 비교적 골고루 부하가 걸려 있는 복합요인을 반영하고 있으며, 요인3은 상권을, 요인 4는 역사와 전통을 나타내고 있다.