인터랙티브 광고의 효과에 관한 연구

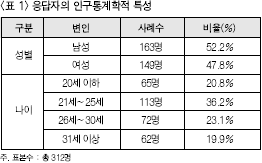
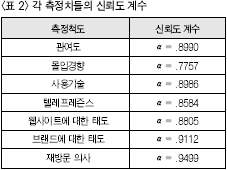
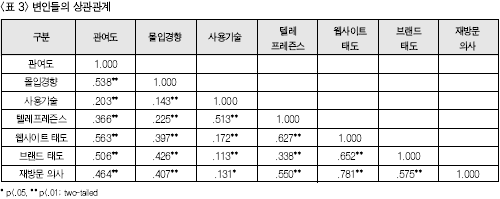
4. 연구결과

1) 기술통계 분석결과

우선 표본으로 선정된 집단의 특성과 응답자들의 기본 특성을 알아보기 위하여 기술 통계를 실시하였는데, 그 결과는 <표 1>과 같다.

다음으로, 각 변인의 측정항목들에 대한 내적일관성을 알아보기 위한 신뢰도 분석을 한 결과, <표 2>에서 보는 바와 같이 .7757에서 .9499까지 대부분의 알파 계수가 높게 나타났다. 따라서, 본 연구에서 얻어진 측정자료들은 신뢰성이 있다고 판단되어 이들 자료들을 이용하여 주어진 가설들을 검증하였다.

그리고, 본 연구에서 가설을 검증하기 위해 사용된 측정문항들의 타당성 검증을 위해서 먼저 각 변인간의 상관분석을 실시하였는데, 분석의 결과는 <표 3>에 자세히 나와 있다.

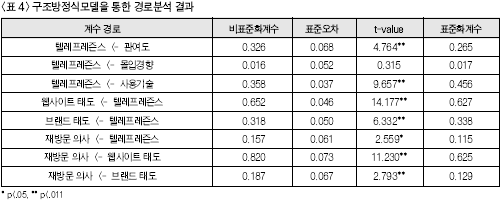
2) 확인적 요인분석 및 연구모델의 적합도 평가

본 연구에서 설정한 가설의 검증을 위하여, 모델의 경로들을 검증하고 모델의 적합도를 살펴보기 위해 AMOS 4.0을 통한 ‘구조방정식모델 분석’ (SEM:structural equation modeling)을 실시하였다. 본 연구에서는 경로분석을 실시하기 전에 ‘확인적 요인분석’ (CFA: confirmatory fac-tor analysis)을 통하여 관찰변인과 잠재변인간의 ‘요인 부하량’ (factor loading,λ)을 측정하였다. 확인적 요인분석은 이론적인 배경 하에서 변인들간의 관계를 설정하고, 요인분석을 이용하여 그 관계가 성립하는 지를 확인하는 방법으로 연구자가 의도한 개념의 측정정도를 직접적으로 평가할 수 있도록 도와준다. 즉, 텔레프레즌스(5문항), 관여도(9문항), 몰입경향(5문항), 사용기술(3문항), 웹 사이트에 대한 태도(5문항), 브랜드에 대한 태도(5문항), 재방문 의사(3문항) 등 7가지 변인에 관련된 총 35문항을 측정하였다. 측정모델에서 관찰변인과 잠재변인간의 관계의 정도를 보여주는 ‘람다(λ) 값’이 0.30보다 크면 적합한 관계를 나타낸다고 할 수 있다(배병렬, 2000, p.9). 측정결과, 모든 관찰변인들이 잠재변인에 대해 만족할만한 ‘요인 부하량’ (λ > 0.30)을 보여주었는데, 지면의 한계로 구체적인 분석결과는 제시하지 않았다.

다음으로, 구조방정식모델을 통한 연구모델의 경로계수 추정치는 다음의 <표 4>와 같다. 이 표에서 각각의 가설 경로에 대하여 ‘최 우추정법’ (MLM: maximum likelihood method)에 의한 경로계수 추정치와 t값(t값=비표준화계수/표준오차)을 보여주고 있는데(표본이 충분히 클 경우, t값≥1.960=Z_0.025에서 유의적임), t값을 이용하여 가설을 검증하였다. 회귀분석에서는 ‘최소자승법’ (least-square)을 이용하여 회귀계수를 구하지만, 구조방정식에서는 구조방정식 계수(λ, Υ, β등)를 구하기 위해서 ‘최우추정법’을 사용한다(오택섭, 최현철, 2004, p.190). 또한, t값이 1.960보다 크거나 같으면 p값은 0.05 수준에서 유의적이라는 것을 나타낸다(김계수, 2002, pp.343-345; 배병렬, 2000, pp.247-248). 즉, t값이 크면 클수록 p값은 낮아지는 것을 뜻하므로, t값만 나타내어도 유의성을 판단할 수 있는 것이다. 한편, 표준화된 계수는 자료를 표준화시켜서 변인간의 상대적인 영향력을 판단하는 기준을 제공해 주는데, 구조방정식모델의 결과에서는 외생변인이 내생변인에게 미치는 영향력의 정도는 ‘감마(Υ)값’으로 나타내고, 내생 변인에서 다른 내생변인에 미치는 영향력의 정도는 ‘베타(β)값’으로 표현한다(오택섭, 최현철, 2004, pp.149-150).

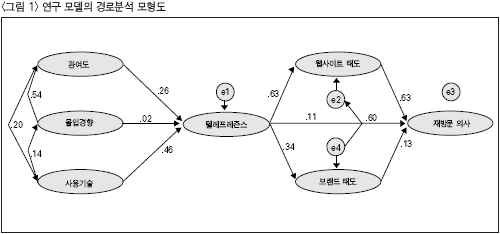
다음으로, 텔레프레즌스의 선행 변인으로서 수용자 변인, 텔레프레즌스, 텔레프레즌스 경험에 따른 인터랙티브 광고의 효과 등 모든 변인간의 관계를 나타내는 통합적인 연구 모델의 적합도를 살펴보았다. Tanaka(1987)는 동일한 모델과 자료가 주어지면 NFI는 ML과 GLS에 따라 불규칙적으로 변화하는 반면, GFI는 두 가지 추정방법에서 일정하게 나타남을 발견하였다. 이러한 결과는 가설화된 모델의 GFI가 0에서 1까지의 범위를 갖기 때문에 NFI 계산에 이용되는 귀무모델의 카이제곱(x²)의 값이 다르기 때문이다. 이러한 결과를 기초로, Tanaka와 Huba(1989)는 유한표본의 경우, ‘구체적인 추정적합지수’ (GFI)가 ‘일반적인 추정적합지수’ (NFI)보다 더 적절하다고 제안하였다. 그들의 이러한 주장은 제한된 상황에서 추정방법에 기초한 정규이론을 근거로 한 것이다(배병 렬, 2000, p. 251).

본 연구에서 설정한 연구 모델의 ‘모델 적합도’를 살펴본 결과 x²=139.2(df = 9), p = 0.000 이며, GFI = 0.902, AGFI = 0.696, CFI = 0.870, RMR = 0.219, RMSEA = 0.216 등으로 나타났다. 즉, 보편적으로 사용하는 적합도 지수인 GFI가 0.902로 나타났는데, 사회과학분야 연구에서 0.800 이상의 논문을 상당수 채택하고 있다는 황용석(1998)의 주장에 비춰보면 괜찮은 모델 적합도를 보여주고 있다고 할 수 있다. 아래의 <그림 1>에서는 연구모델의 경로분석 모형도를 보여주고 있다.

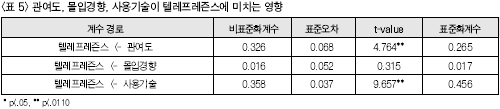
3) 가설의 검증결과

<가설 1-1>은 “소비자의 관여도가 높을수록 텔레프레즌스의 경험정도가 더 높을 것이다”이고, <가설 1-2>는 “소비자의 몰입경향이 높을수록 텔레프레즌스의 경험정도가 더 높을 것이다”이며, <가설 1-3>는 “소비자의 인터랙티브 광고의 사용기술의 정도가 높을수록 텔레프레즌스의 경험정도가 더 높을 것이다”였는데, 이러한 가설에 대한 검증 결과를 살펴보면 다음의 <표 5>와 같다.

<가설 1-1>의 경우, Υ=0.265, t=4.764로써 가설이 채택되었다. 즉, 소비자의 인터랙티브 광고에 대한 관여도가 높을수록 텔레프레즌스의 경험 정도가 더 높아진다는 것을 의미한다. 이러한 결과는 Novak 등(1998)의 연구결과와 일치하는 것으로, 소비자들의 인터랙티브 광고에 대한 관여도가 높으면 이용자들의 집중된 주목을 불러일으키므로 텔레프레즌스의 경험정도도 높아진다는 사실을 뒷받침해주고 있다. 그리고, <가설 1-2>의 경우, Υ=0.017, t=0.315로써 가설이 기각되었는데, 이것은 소비자의 몰입경향이 높을수록 텔레프레즌스의 경험정도가 높아진다는 가설이 통계적으로 유의미하지 않음을 나타내 주는 것이다. 즉, 소비자의 몰입경향은 텔레프레즌스의 경험정도에 영향을 미치지 않는 것으로 나타났다. 이와 같은 결과는 선행연구인 Witmer와 Singer(1998)의 연구와는 상반된 결과이며, 마정미(2002)의 연구와는 동일한 결과를 보여주고 있다. 이러한 결과는 몰입경향의 척도가 외국에서 개발된 것이기에 한국의 실정에는 맞지 않기 때문에 발생했을 가능성도 있을 것이다. 따라서, 수용자 변인에 있어서의 척도 개발, 특히 몰입경향에 대한 척도는 한국의 실정에 맞게 개발되어야 할 것이라고 생각된다.

다음으로, <가설 1-3>의 경우, Υ=0.456, t=9.657로써 가설이 채택되었다. 즉, 소비자의 사용 기술의 정도가 높을수록 텔레프레 즌스 경험의 정도가 더 높아질 것이라는 것을 의미한다. 이러한 결과는 선행연구들(황용석, 1998; Novak, Hoffman, & Yung, 1998; Trevino & Webster, 1992)과 일치하고 있다. 이는 3D의 인터랙티브광고를 보는데 있어서, 사용 경험이 많아 사용하는데 생소하지 않고 친숙함을 느낀다거나 사용 숙련도가 높으면 그만큼 텔레프레즌스를 경험할 확률도 더 높아진다는 것을 나타낸다. 또한, 사용기술의 정도가 크면 클수록 사용의 용이함을 가져와서 능숙하게 이용할 수 있으므로, 통제나 주목의 정도가 높아진다는 사실을 뒷받침해 준다고 할 수 있다.

한편, <가설 2-1>은 “텔레프레즌스의 경험정도가 높을수록 소비자의 웹사이트에 대한 태도가 더 호의적일 것이다”이고, <가설 2-2>는 “텔레프레즌스의 경험정도가 높을수록 소비자의 브랜드에 대한 태도가 더 호의적일 것이다”이며, <가설 2-3>은 “텔레프레즌스의 경험정도가 높을수록 소비자의 재방문 의사가 더 높을 것이다”였는데, 이러한 가설에 대한 검증결과를 살펴보면 <표 6>과 같다.

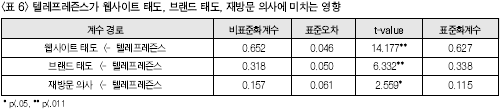
<가설 2-1>의 경우, β=0.627, t=14.177로써 가설이 채택되었다. 이는 인터랙티브 광고에 있어 텔레프레즌스의 경험정도가 높을수록 소비자의 웹사이트에 대한 태도가 더 호의적이라는 것을 의미한다. <가설 2-2>의 경우 β=0.338, t=6.332로써 가설이 채택되었다. 즉, 인터랙티브 광고에 있어 텔레프레즌스의 경험정도가 높을수록 소비자의 브랜드에 대한 태도가 더 호의적일 것이라는 것을 나타낸다. 그리고 <가설 2-3>의 경우 β=0.115, t=2.559로써 가설이 채택되었다. 따라서, 인터랙티브 광고에 있어 텔레프레즌스의 경험정도가 높을수록 소비자의 재방문 의사도 더 높아진다는 것을 의미한다. 이러한 연구결과들 역시 텔레프레즌스의 경험이 광고효과에 영향을 미친다는 선행연구들(최영균, 2003; Choi, 2000; Choi, Miracle, & Biocca, 2001; Kim, 1996; Kim & Biocca, 1997; Li, Daugherty, & Biocca, 2002)과 일치하는 것으로서, 텔레프레즌스 경험이 각각 기억과 설득, 웹사이트에 대한 태도, 광고에 대한 태도, 브랜드에 대한 태도, 브랜드 구매의사, 재방문 의사 등에 긍정적인 영향을 미친다는 사실을 입증해주고 있다. 그리고,

<가설 2-4>는 “소비자의 웹사이트에 대한 태도가 호의적일수록 재방문 의사가 더 높을 것이다”이고, <가설 2-5>는 “소비자의 브랜드에 대한 태도가 호의적일수록 재방문 의사가 더 높을 것이다”였는데, 이러한 가설에 대한 검증결과를 살펴보면 <표 7>과 같다. <가설 2-4>의 경우, β=0.625, t=11.230으로써 가설이 채택되었다. 즉, 이는 인터랙티브 광고에 있어 웹사이트에 대한 태도가 호의적일수록 재방문 의사가 더 높아진다는 것을 의미한다. 그리고, <가설 2-5>의 경우 β=0.129, t=2.793으로써 가설이 채택되었다. 이는 인터랙티브 광고에 있어 브랜드에 대한 태도가 호의적일수록 재방문 의사가 더 높아진다는 것을 나타낸다. 이러한 연구 결과들을 살펴보면, 인터랙티브 광고에 있어 웹사이트에 대한 태도 및 브랜드에 대한 태도가 호의적일수록 재방문 의사가 높아진다고 할 수 있다.

이와 더불어, 본 연구에서는 추가적으로 텔레프레즌스가 재방문 의사에 미치는 영향력을 자세히 살펴보기 위하여 공변량을 분해해 보았다. 즉, 텔레프레즌스에서 재방문 의사로 영향을 미치는 직접적인 효과와 텔레프레즌스에서 웹사이트에 대한 태도 및 브랜드에 대한 태도를 거쳐 재방문 의사로 영향을 미치는 간접적인 효과를 비교해 보았다. 그 결과, 텔레프레즌스에서 재방문 의사로 미치는 전체 효과계수는 0.550으로 나타났으며, 텔레프레즌스에서재방문 의사로 미치는 직접적인 효과는 0.115, 그리고 텔레프레즌스에서 재방문 의사로 미치는 간접적인 효과는 0.435로 나타났다. 또한, 여기에서의 간접효과는 텔레프레즌스가 웹사이트에 대한 태도에 미치는 직접적인 효과인 0.63과 웹사이트에 대한 태도가 재방문 의사에 미치는 직접적인 효과인 0.63을 곱한 값과 텔레프레즌스가 브랜 드에 대한 태도에 미치는 직접적인 효과인 0.34와 브랜드에 대한 태도가 재방문 의사에 미치는 직접적인 효과인 0.13을 곱한 값을 더한 것이다. 이러한 결과들에 비추어 보면, 텔레프레즌스가 재방문 의사에 미치는 효과는 직접적인 효과(0.115)보다 간접적인 효과(0.435)가 더 크다는 것을 알 수 있다. 즉, 텔레프레즌스가 재방문 의사에 직접적으로 영향을 미치는 직접적인 효과보다는 웹사이트에 대한 태도 및 브랜드에 대한 태도를 거쳐 간접적으로 영향을 미치는 간접효과가 더 크다는 것을 의미한다.

다음 페이지로