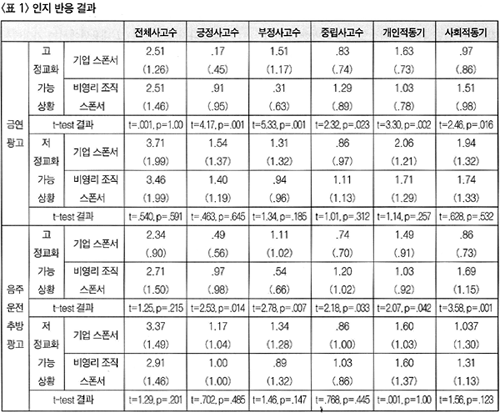
5. 연구 결과 및 논의본 연구는 세 가지 연구문제를 설정하고 이에 대한 답을 얻기 위하여 가설들을 설정하였다. 먼저 첫 번째 연구문제는 소비자가 공익 광고의 내용을 정교화 할 수 있는 상황 여부 및 공익 광고의 스폰서 유형이 공익 광고에 대한 인지 반응에 영향을 미치는가를 알아보는 것이다. 이에 대한 답을 구하기 위하여 <가설 1-1>과 <가설 1-2>를 설정하였다. 구체적으로 <가설 1-1>은 정교화가 활발히 일어날 수 있는 상황에 관한 것으로 이 경우 기업이 스폰서 하는 공익 광고에 접한 소비자는, 특히 그 공익 광고가 기업의 제품 판매에 부정적인 영향을 초래할 수 있을 경우, 비영리 조직이 스폰서 하는 공익광고에 접한 소비자보다 복잡한 인지과정을 거쳐 보다 많은 의구심을 유발할 것이기 때문에 전체 사고 수도 많을 것이고 긍정적 사고보다 부정적 사고가 많을 것으로 예상한 것이다. 또한 이 경우 비영리 조직이 스폰서 하는 광고에 접한 소비자는 사회적 차원의 동기를, 영리 기업이 스폰서 하는 광고에 접한 소비자는 개인적 차원의 동기를 보다 많이 유발할 것으로 예상하였다. 연구 결과 금연 광고와 음주운전 추방 광고를 실험 처치물로 한 경우 모두 전체 사고의 수에서는 통계적으로 유의미한 차이가 없었다(t=.001, p=1.00; t=1.25, p= .215). 그러나 그 내용을 보면 금연 광고를 실험 처치물로 한 경우 긍정적(t=4.17, p=.001), 부정적(t=5.33, p=.001) 사고의 수, 개인적(t=3.30, p=002), 사회적 (t=2.46, p= .016) 동기 모두에서 두 집단 간에 유의미한 차이가 나타났으며, 음주운전 추방 광고를 실험 처치물로 한 경우에도 금연 광고에서와 같이 두 집단 간에 통계적으로 유의미한 차이가 나타났다(긍정적 -t=2.53, p= .014: 부정적 -t=2.78, p= .007 ; 개인적 -t=2.07, p= 0.42; 사회적 -t=3.58, p= .001). 따라서 <가설 1-1>은 부분적으로 지지되었다고 할 수 있다. 한편 <가설 1-2>는 정교화가 활발히 일어날 수 없는 상황에 관한 것인데, 이 경우에는 공익 광고의 스폰서 유형에 따라 전체 사고의 수, 긍정적, 부정적 사고의 수 및 개인적, 사회적 동기의 수에 있어 유의미한 차이가 나타나지 않을 것으로 예상하였다. 연구결과 금연 광고 및 음주운전 추방 광고 모두의 경우에 전체 사고의 수(금연 광고 -t= .540, p= .591, 음주운전 추방 광고 -t= 1.29, p=.201), 긍정적(금연 광고 -t=.463, p= .645; 음주운전 추방 광고 -t= .702, p= .485), 부정적 사고의 수(금연 광고 -t=1.34, p= .185; 음주운전 추방 광고 -t= 1.46, p=.147), 개인적(금연 광고 -t=1.14, p= .257; 음주운전 추방 광고 -t= .001, p=1.00) , 사회적 동기의 수(금연 광고 -t= .628, p= .532; 음주운전 추방 광고 -t=1.56, p= .123)에서 통계적으로 유의미한 차이가 나타나지 않았다. 따라서 <가설 1-2>은 지지되었다고 할 수 있다(<표 1> 참고).
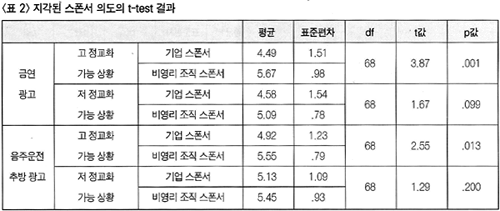
이상과 같은 연구 결과는 정교화 수준에 따라 인지 반응 수에서는 차이가 없었으나 그 내용에 있어서는 차이가 있음을 보여주었다. 즉 정교화가 활발히 일어날 수 있는 상황의 경우엔 공익 광고의 스폰서가 영리적 기업일 경우 전체 사고 수면에서도 비영리 조직이 스폰서하는 경우보다 많고, 부정적 사고가 긍정적 사고보다, 그리고 개인적 동기가 사회적 동기보다 많이 유발될 것으로 예상하였다. 연구 결과 전체 사고 수에서는 차이가 나타나지 않았으나 그 내용면에서는 가설에서 예상한 바와 같은 결과가 나타났다. 반면 정교화가 활발히 일어날 수 없는 상황의 경우엔 가설에서 예상한 바와 같이 스폰서의 유형에 따라 인지반응의 수, 사고의 내용면에서 차이가 없었다. 이상과 같이 인지 반응의 내용면에서 나타난 결과에 가설에도 명시하였듯이 스폰서의 의도에 대한 의구심이 유발될 경우 스폰서에 대한 복잡한 귀인 과정을 거치게 되며, 이 과정에서 긍정적 보다는 부정적 사고가, 또 사회적 동기보다는 개인적 동기가 촉발되기 쉽다는 것을 보여주는 것으로 설득 지식 모델 및 선행 연구 결과를 뒷받침해주는 결과라고 할 수 있다(Campbell & Kirmani, 2000'; Szykman, Bloom, & Blazing, 2004). 두 번째 연구문제는 소비자가 공익 광고의 내용을 정교화 할 수 있는 상황 여부 및 공익 광고의 스폰서 유형이 스폰서의 의도에 대한 소비자 각각에 영향을 미치는가를 알아보는 것이다. 이를 위해 <가설 2-1>과 <가설 2-2>를 설정하였다. 먼저 <가설 2-1>은 정교화가 활발히 일어날 수 있는 상황의 경우 공익 광고의 스폰서가 영리적 기업인가 또는 비영리 조직인가에 따라 소비자가 공익 광고 스폰서의 의도를 다르게 평가할 것으로 예상하고 설정한 것이다. 가설 검증 결과 금연 광고(t=3.87, p= .001) 및 음주운전 추방 광고(t=2.55, p=.013)의 경우 모두 통계적으로 유의미한 결과가 나타났다. 따라서 <가설 2-1>은 지지 되었다고 할 수 있다. 한편 <가설 2-2>는 정교화가 활발히 일어날 수 없는 상황의 경우 스폰서의 유형에 따라 소비자가 스폰서의 의도를 어떻게 지각하는가에 차이가 없을 것으로 예상하고 설정된 것이다. 검증 결과 금연 광고(t=1.67, p= .099) 및 음주운전 추방광고(t=1.29, p= .200) 모두의 경우에 두 집단 간에 유의미한 차이가 나타나지 않음으로써 <가설 2-2>도 지지되었다고 할 수 있다(<표 2> 참고).
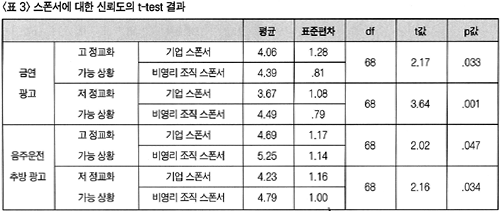
이상의 연구 결과는 앞서 지적한 바와 같이 설득 지식 모델의 가정과 이를 다룬 선행 연구의 결과와 일치하는 것이다(Campbell & Kirmani, 2000: Friestad & Wright, 1994). 즉 설득 지식 모델에서는 소비자가 살아오면서 설득 지식을 계발, 축적해가며, 이를 토대로 설득 상황에서 마케터의 동기에 대한 추론을 한다. 이 추론 과정에서, 특히 소비자가 상충되는 마케터의 동기들을 인지하게 되면 의구심을 유발하며, 이는 궁극적으로는 마케터가 전달하는 설득 메시지의 효과에 부정적인 영향을 미치게 된다. 그런데 이러한 추론은 특히 소비자가 설득 메시지를 의식적으로 정교화할 수 있는 상황에서 활발히 발생한다. <가설 2-1>과 <가설 2-2>의 연구 결과는 이러한 선행 연구 결과를 뒷받침해주는 것으로 정교화 상황에 따라 소비자가 스폰서의 의도를 어떻게 지각하는가가 다르게 나타남을 보여준 것이라 하겠다. 즉 정교화가 활발히 발생할 수 있는 상황에서 소비자는, 특히 본 연구에서와 같이 기업이 스폰서하는 공익 광고의 내용이 기업 이익에 부정적인 영향을 초래할 수 있는 경우, 비영리 조직이 스폰서하는 경우 보다 스폰서의 의도를 통계적으로 유의미하게 낮게 평가하였다. 반면에 정교화가 활발히 발생할 수 없는 상황에서는 두 집단의 응답 간에 유의미한 차이가 없었다. 세 번째 연구문제는 공익 광고의 스폰서 유형이 공익 광고에 대한 소비자 반응에 영향을 미치는 가를 알아보는 것이다. 이를 위해 <가설 3-1>, <가설 3-2>와 <가설 3-3>을 설정하였다. 우선 <가설 3-1> 에서는 영리적 기업이 스폰서하는 공익 광고에 접한 소비자는 비영리 조직이 스폰서하는 공익 광고에 접한 소비자 보다 스폰서에 대한 신뢰도를 부정적으로 평가할 것으로 예상하였다. 검증 결과 금연 광고 및 음주운전 추방 광고 모두의 경우에 비영리 조직이 스폰서하는 공익 광고에 접한 소비자가 영리적 기업이 스폰서하는 공익 광고에 접한 소비자 보다 스폰서에 대한 신뢰도를 통계적으로 유의미하게 긍정적으로 평가하는 것으로 나타났다. 구체적으로 두 집단 간의 차이를 검증한 결과 금연 광고의 경우 높은 정교화 상황(t=2.17, p= .033), 낮은 정교화 상황(t=3.64, p= .001), 음주운전 추방 광고의 경우 높은 정교화 상황(t=2.02, p=.047), 낮은 정교화 상황(t=2.16, p=.034) 모두 유의미하게 나타났다(<표 3> 참고). 따라서 <가설 3-1>은 지지되었다고 하겠다.
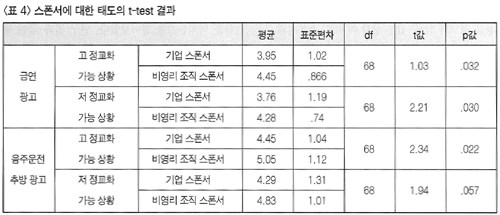
<가설 3-2>에서는 비영리 조직이 스폰서하는 공익 광고에 접한 소비자는 영리적 기업이 스폰서하는 공익 광고에 접한 소비자보다 스폰서에 대해 긍정적인 태도를 지닐 것으로 예상하였다. 검증 결과 금연 광고 및 음주운전 추방 광고 모두의 경우에 비영리 조직이 스폰서하는 공익 광고에 접한 소비자가 영리적 기업이 스폰서하는 공익 광고에 접한 소비자보다 스폰서에 대한 태도를 통계적으로 유의미하게 긍정적으로 평가하는 것으로 나타났다. 구체적으로 두 집단 간의 차이를 검증한 결과 금연 광고의 경우 높은 정교화 상황(t=2.18, p= .032)과 낮은 정교화 상황 (t=2.21, p= .030) , 음주운전 추방 광고의 경우, 높은 정교화 상황(t=2.34, p= .022)과 낮은 정교화 상황(t=1.94, p=.057) 모두 유의미하게 나타났다(<표 4> 참고). 따라서 <가설 3-2>도 지지되었다고 하겠다.
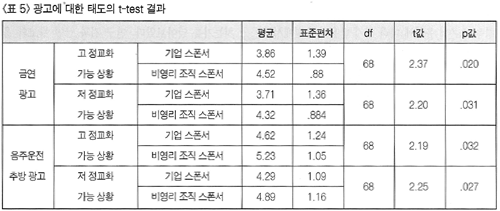
<가설 3-3>에서는 비영리 조직이 스폰서하는 공익 광고에 접한 소비자는 영리적 기업이 스폰서하는 공익 광고에 접한 소비자보다 광고에 대해 긍정적인 태도를 지닐 것으로 예상하였다. 검증 결과 금연 광고 및 음주운전 추방 광고 모두의 경우에 비영리 조직이 스폰서하는 공익 광고에 접한 소비자가 영리적 기업이 스폰서하는 공익 광고에 접한 소비자 보다 스폰서에 대한 태도를 통계적으로 유의미하게 긍정적으로 평가하는 것으로 나타났다. 구체적으로 두 집단 간 차이를 검증한 결과 금연 광고의 경우 높은 정교화 상황(t=2.20, p= .020)과 낮은 정교화 상황(t=2.20, p= .031), 음주운전 추방 광고의 경우 높은 정교화 상황(t=2.19, p= .032)과 낮은 정교화 상황(t=2.25, p= .027) 모두 유의미하게 나타났다(<표 5> 참고).
따라서 <가설 3-3>도 지지되었다고 하겠다. 요컨대 이상과 같은 <가설 3-1>, <가설 3-2>, <가설 3-3>의 검증 결과는 스폰서 유형에 따라 공익 광고에 대한 소비자 반응이 다르게 나타남으로써 스폰서 유형이 공익 광고의 효과에 영향을 미치는 중요한 요인임을 보여준 것으로 해석할 수 있다. 여기서 공익 광고의 스폰서는 앞서 언급하였듯이 소비자에게 정보원의 역할을 한다고 볼 수 있다. 따라서 이러한 결과는 설득 지식 모델의 가정을 지지해줄 뿐만 아니라, 정보원을 다룬 선행 연구들(김정현, 김자경, 2002; Goldsmith, Lafferty, & Newell, 2000)에서 보여준 바와 같이 정보원이 광고 효과에 영향을 미치는 주요 요인 가운데에 하나임을 보여준 결과라고 할 수 있다. |
|
|
|
|
|
|